El número de oro:
la relación entre lo divino, la naturaleza y el hombre.
¿Es posible pensar la relación entre la
divinidad, la naturaleza y la razón humana?
Lo es en muchos sentidos, pero el hombre siempre busca evidencias.
Bueno, las evidencias son matemáticamente posibles.
Einstein sostenía que "Dios no juega a
los dados."
Veamos:
La "divina proporción" o número de
oro conocido como número áureo o razón media se representa con la letra
griega phi (Φ,φ) es un número algebraico irracional (φ=1,61...) usado por los
griegos y fue aplicado desde la antigüedad como proporción a la construcción
y al arte.
Pero se ha descubierto que este número no
sólo es propio del uso racional humano, como en las figuras geométricas y en
la sucesión de Fibonacci (matemático del s. XIII); o también artistas y
diseñadores del siglo XX que han hecho uso de la "divina
proporción".
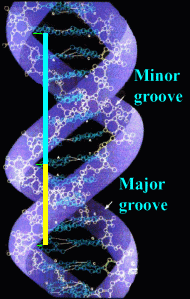
Existe como proporción en las formas de la
naturaleza: nervaduras de las hojas de algunos árboles, caparazón de
caracoles, las telas de araña, etc., incluso la estructura helicoidal del
ADN. Recientemente se han descubierto galaxias cuya forma repite el número de
oro.
|
La proporción áurea está en todas partes:
En
la naturaleza. Hay muchos elementos relacionados con la sección áurea o
la secuencia de Fibonacci que tienen una gran similitud. La
disposición de los pétalos de las flores, La distribución de las
hojas en un tallo. La relación entre las nervaduras
de las hojas de los árboles. La relación entre el grosor de las
ramas principales y el tronco, o entre las ramas principales y las secundarias.
La cantidad de espirales de una piña.
Estos números son
elementos de la sucesión de Fibonacci y el cociente de dos elementos
consecutivos tiende al número áureo. En la cantidad de pétalos en las flores
existen por ejemplo flores con 3, 5 y 8 pétalos y también con 13, 21, 34, 55,
89 y 144. Está en el ADN y así podemos descubrirlo en infinidad
de ejemplos más. Habitualmente se ejemplifica con la caparazón del nautilus o con las caparazones de los caracoles.
Sin embargo, podemos dar muchísimos otros ejemplos en nuestro planeta. Por caso, los huracanes, responden a esta proporción.
Fuera del planeta, en el espacio, también encontramos galaxias cuya forma sigue la regla de la proporción áurea.
En el cuerpo humano. Resulta que el
cociente entre la altura del hombre y la
distancia del ombligo a la punta de la mano es el número áureo. La más llamativa
tal vez sea la relativa al ombligo: si se divide la altura total de un hombre
entre la distancia del ombligo a los pies obtenemos el número áureo. En la
investigación sobre la odontología se ha demostrado que la dentadura va
creciendo según la proporción áurea. En nuestras manos las falanges están en
sucesión áurea 6.
En
las artes plásticas. Aparece
en el siglo V a C en Atenas, los griegos lo conocían y utilizaban en los
diseños arquitectónicos y escultóricos. Una de las construcciones más famosas
en las que se ha utilizado es el Partenón. También encontramos las
proporciones del rectángulo áureo y sus secciones en el Edificio
de la O.N.U en Nueva York, la Torre Eiffel, los rosetones góticos y la pintura del Renacimiento, así como en muchísimas obras de artistas del siglo XX.
En
la música. En
varias sonatas para piano de Mozart,
la proporción entre el desarrollo del tema y su introducción es la más cercana
posible a la razón áurea. Aunque no se sabe que Beethoven estuviera al tanto de esto, en su Quinta
Sinfonía, distribuye el tema siguiendo la sección áurea. En
instrumentos como el piano, ya que está constituido por siete
octavas ordenadas de forma creciente de graves a agudas. Así, los primeros seis
números de la Sucesión de Fibonacci,
muy similar a la proporción áurea, figuran en una octava de piano, la cual
consiste en 13 teclas: 8 teclas blancas y 5 teclas negras, en grupos de 2 y 3.
En
las matemáticas. El
número de oro o proporción áurea están presentes en todos los
objetos geométricos regulares
o semiregulares en los que haya simetría pentagonal, que sean pentágonos o que
aparezca de alguna manera la raíz cuadrada de cinco. Está relacionado con los sólidos
platónicos, en particular con el icosaedro y el dodecaedro,
cuyas dimensiones están dadas en términos del número de oro.
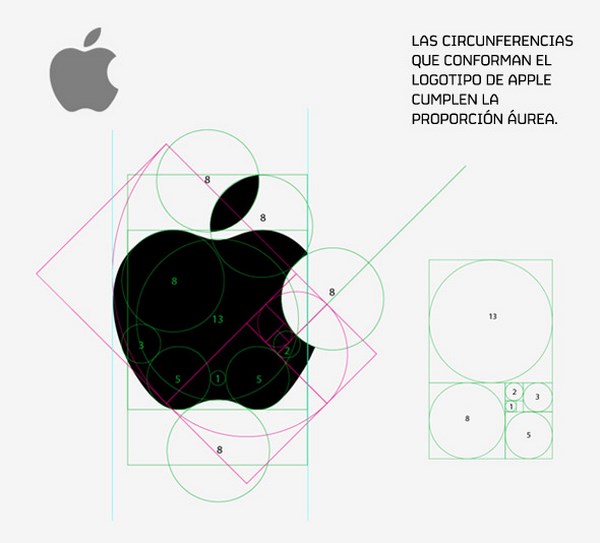
Incluso objetos contemporáneos y logotipos, marcas, etc. han sido diseñados utilizando la proporción áurea:
Vídeo: La divina proporción
Si el tema resultó de interés, pueden consultar:
No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.